题目内容
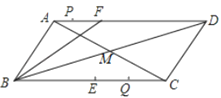
【题目】在数学拓展课上，老师让同学们探讨特殊四边形的做法：
如图，先作线段
，作射线
（
为锐角），过
作射线
平行于，再作和
的平分线分别交和于点
和
，连接
，则四边形
为菱形；
（1）你认为该作法正确吗？请说明理由.
（2）若
，并且四边形的面积为
，在
上取一点
，使得
.请问图中存在这样的点吗？若存在，则求出
的长；若不存在，请说明理由.
【答案】（1）作法正确（2）
或
【解析】
（1）根据作法可以推出
，又因为
，所以四边形
是平行四边形，又
，所以四边形是菱形，因此作法正确；
（2）作
，由面积公式可求出
,由菱形的性质可得AD=AB=4，用勾股定理可得
，由锐角三角函数得
，所以
是正三角形.再根据菱形对角线互相垂直的性质，利用勾股定理解得
或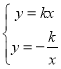
.
（1）作法正确.理由如下：
∵
∴
∵
平分
，
平分
∴
∴
∴
又∵
∴四边形是平行四边形
∵
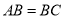
∴四边形是菱形.
故作法正确.
（2）存在.
如图，作
∵
， 
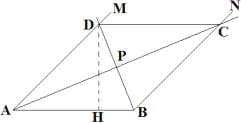
∴ 且
∴由勾股定理得
∴由锐角三角函数得
∴是正三角形
∴
∵
∴
∴或
练习册系列答案
相关题目
【题目】如图，均匀的正四面体的各面依次标有1，2，3，4四个数字，小明做了60次投掷试验，结果统计如下：
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
（1）求上述试验中“2朝下”的频率；
（2）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于5的概率．
