题目内容
【题目】顶点为（﹣ 
，﹣ 
）的抛物线与y轴交于点A（0，﹣4），E（0，b）（b＞﹣4）为y轴上一动点，过点E的直线y=x+b与抛物线交于B、C两点．
（1）求抛物线的解析式；
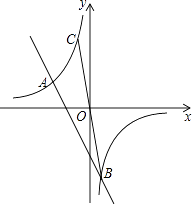
（2）①如图1，当b=0时，求证：E是线段BC的中点；
②当b≠0时，E还是线段BC的中点吗？说明理由．
【答案】
（1）
解：据题意可设抛物线的解析式为y=a（x+ 
）2﹣ 
．
把x=0，y=﹣4代入，得﹣4=a（0+ ）2﹣ ，
解得a=1，
∴抛物线的解析式为y=（x+ ）2﹣ =x2+x﹣4．
（2）
①证明：分别过点B、C作BM⊥y轴于点M，CN⊥y轴于点N．（如图1）
当b=0时，直线BC为y=x，此时点E与点O重合．
由方程组 
，
得 
， 
．
则B、C的坐标分别为（2，2）、（﹣2，﹣2），
即BM=CN=2．
又BM⊥y轴，CN⊥y轴，
∴BM∥CN，
∴△BME∽△CNE，
即BE：CE=BM：CN，
故BE=CE．
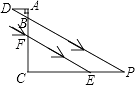
②解：E还是线段BC的中点．理由如下：
如图2，分别过点B、C作BP⊥y轴于点P，CQ⊥y轴于点Q．
由方程组 
，
得 
， 
．
则B、C的坐标分别为（ 
， +b），（﹣ ，﹣ +b），
即BP=CQ= ．
同样可得△BPE∽△CQE，
即BE：CE=BP：CQ，
故BE=CE
【解析】（1）因为知道抛物线的顶点坐标，所以可设抛物线的解析式为：y=a（x+ x）2﹣ ，把A点的坐标代入求出a的值即可求出抛物线的解析式；（2）①分别过点B、C作BM⊥y轴于点M，CN⊥y轴于点N，当b=0时，直线BC为y=x，此时点E与点O重合，联立直线和抛物线的解析式可求出B，C点的坐标，进而得到BM=CN=2，再通过证明△BME∽△CNE，由相似三角形的性质可得：BE：CE=BM：CN，故BE=CE；②当b≠0时，E还是线段BC的中点，分别过点B、C作BP⊥y轴于点P，CQ⊥y轴于点Q，其他过程同①．
【考点精析】本题主要考查了相似三角形的性质的相关知识点，需要掌握对应角相等，对应边成比例的两个三角形叫做相似三角形才能正确解答此题．
