Question

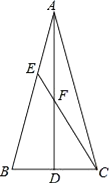
【题目】如图，在△ABC中，∠BAC=30°，AB=AC，AD是BC边上的中线，∠ACE=∠BAC，CE交AB于点E，交AD于点F．若BC=2，则EF的长为__．

Answer 1

【答案】﹣1

【解析】过F点作FG∥BC,∵在△ABC中,AB=AC,AD是BC边上的中线,

∴BD=CD==1,∠BAD=∠CAD=∠BAC=15°,AD⊥BC,

∵∠ACE=∠BAC,∴∠CAD=∠ACE=15°,∴AF=CF,

∵∠ACD=（180°-30°）÷2=75°,∴∠DCE=75°-15°=60°,

在Rt△CDF中,AF=CF==2,DF=CDtan60°=,

∵FG∥BC,∴GF：BD=AF：AD,即GF：1=2：（2+）,解得GF=4-2,

∴EF：EC=GF：BC,即EF：（EF+2）=（4-2）：2,解得EF=﹣1

故答案为:﹣1.