题目内容

抛物线y=x2-（b-2）x+3b的顶点在y轴上，则b的值为
 
．
分析：把抛物线解析式转化为顶点形式，即可得顶点坐标，再根据顶点在y轴上，即x=0，即可得b的值．
解答：解：根据题意，把解析式转化为顶点形式为：
y=x2-（b-2）x+3b=（x-
b-2
2
）2+3b-（
b-2
2
）2，
顶点坐标为（
b-2
2
，3b-（
b-2
2
）2），
∵顶点在y轴上，
∴
b-2
2
=0，
∴b=2．
点评：本题考查了二次函数图象与系数关系，是基础题型．
练习册系列答案
相关题目
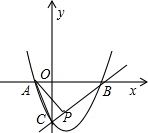如图，直线y=x-3于x轴、y轴分别交于B、C；两点，抛物线y=x2+bx+c同时经过B、C两点，点精英家教网A是抛物线与x轴的另一个交点．
（1）求抛物线的函数表达式；
（2）若点P在线段BC上，且S△PAC=
12
S△PAB，求点P的坐标．
已知x1、x2是抛物线y=x2-2（m-1）x+m2-7与x轴的两个交点的横坐标，且x12+x22=10．
求：（1）x1、x2的值；
（2）抛物线的顶点坐标．
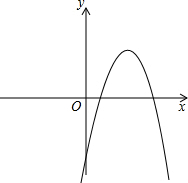精英家教网已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
（1）求b、c的值（用含m的代数式表示）；
（2）设抛物线y=-x2+bx+c与x轴交于A、B两点，与y轴交于点C．若点D的坐标为（0，-2），且AD•BD=10，求抛物线的解析式及点C的坐标；
（3）在（2）中所得的抛物线上是否存在一点P，使得PC=PD？若存在，求出P点的坐标；若不存在，请说明理由．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是
2
．（写出一个即可）
11、在平面直角坐标系中，将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°，所得抛物线的解析式是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网