Question

【题目】在平面直角坐标系中，点的坐标分别为且满足，连接.

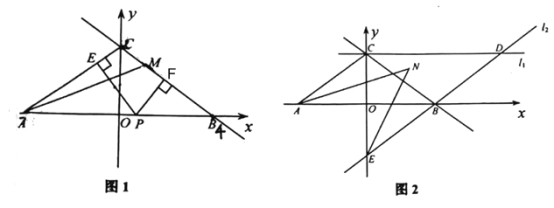
（1）如图1，若，点是直线上的一个动点，当最短时，求的值； 点是线段上的一个动点，且满足于点，于点，求的值；

（2）如图2，过点作直线轴，过点作，与交于点，与轴交于点，分别平分，求的度数.

Answer 1

【答案】（1）最短时，的值为；；（2）∠ANE=45°.

【解析】

（1）根据非负数的性质可求出a，b，得到点A，B的坐标，过点A作AM’⊥BC于点M’，AM最短时即为AM’，然后根据可求出AM’的长；连结CP，根据可求出；

（2）过点N作NG∥AC，则NG∥AC∥BE，根据平行线的性质和角平分线的定义可求出∠ANE=∠ANG+∠GNE=∠CAN+∠BEN=(∠CAB+∠CEB)= (∠CAB+∠ACO)=45°.

解：（1）∵，

∴a+4=0，b-4=0，

∴a=－4，b=4，

∴，

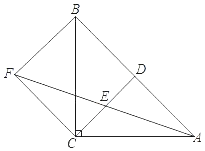
如图，过点A作AM’⊥BC于点M’，AM最短时即为AM’，

∵，即8×3=5 AM’，

∴AM’=，即最短时，的值为；

连结CP，

∵

∴，

∴；

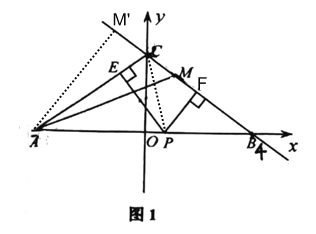
（2）过点N作NG∥AC，则NG∥AC∥BE，

∴∠ACO=∠CEB，∠CAN=∠ANG，∠BEN=∠GNE，

∵AN，EN分别平分，

∴∠CAN=∠CAB，∠BEN=∠CEB，

∴∠ANE=∠ANG+∠GNE=∠CAN+∠BEN=(∠CAB+∠CEB)= (∠CAB+∠ACO)=45°.