题目内容
把下列代数式分别填入它们所属的集合中:
m2-m,-x2-2x+1,y,
,-
,
,π,a-b.
单项式集合{
多项式集合{
m2-m,-x2-2x+1,a-b
m2-m,-x2-2x+1,a-b …}
整式集合{
m2-m,-x2-2x+1,y,-
,
,π,a-b
m2-m,-x2-2x+1,y,-
,
,π,a-b …}.
| 2 |
| 5 |
| 7 |
| x-1 |
| 1 |
| 4 |
| ab2c3 |
| 5 |
单项式集合{
y,-
,
,π
| 1 |
| 4 |
| ab2c3 |
| 5 |
y,-
,
,π
…}| 1 |
| 4 |
| ab2c3 |
| 5 |
多项式集合{
| 2 |
| 5 |
| 2 |
| 5 |
整式集合{
| 2 |
| 5 |
| 1 |
| 4 |
| ab2c3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 4 |
| ab2c3 |
| 5 |
分析:根据单项式与多项式的定义即可判断.
解答:解:单项式集合{ y,-
,
,π …}
多项式集合{
m2-m,-x2-2x+1,a-b …}
整式集合{
m2-m,-x2-2x+1,y,-
,
,π,a-b,…}.
故答案是:y,-
,
,π;
m2-m,-x2-2x+1,a-b;
m2-m,-x2-2x+1,y,-
,
,π,a-b.
| 1 |
| 4 |
| ab2c3 |
| 5 |
多项式集合{
| 2 |
| 5 |
整式集合{
| 2 |
| 5 |
| 1 |
| 4 |
| ab2c3 |
| 5 |
故答案是:y,-
| 1 |
| 4 |
| ab2c3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 4 |
| ab2c3 |
| 5 |
点评:主要考查了整式的有关概念.要能准确的分清什么是整式.整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除式不能含有字母.单项式和多项式统称为整式.单项式是字母和数的乘积,只有乘法,没有加减法.多项式是若干个单项式的和,有加减法.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
把下列代数式分别填入下表适当的位置:3a,
,
,
+b,5,-xy,a2-2ab+1.
| 3 |
| a |
| a-b |
| 2 |
| a |
| 代数式 | 整式 | 单项式 | |
| 多项式 | |||
| 非整式 | |||
把下列代数式分别填入下表适当的位置:3a, ,
,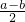 ,
, ,5,-xy,a2-2ab+1.
,5,-xy,a2-2ab+1.
| 代数式 | 整式 | 单项式 | |
| 多项式 | |||
| 非整式 | |||