题目内容
已知：如图，E、F分别为?ABCD中AD、BC的中点，分别连接AF、BE交于G，连接CE、DF交于点H．求证：EF与GH互相平分．
证明：∵E为AD的中点，F为BC的中点，
∴AE=
AD，CF=BC，
∵四边形ABCD是平行四边形，
∴AD∥BC，∴AE∥CF，AE=CF，
∴四边形AFCE是平行四边形，
∴AF∥CE，
同理可证：BE∥DF，
∴四边形GFHE是平行四边形，
∴EF与GH互相平分．
分析：可先求解四边形AFCE是平行四边形，进而利用平行四边形的性质得出四边形GFHE是平行四边形，即可得出结论．
点评：本题主要考查平行四边形的判定问题，能够熟练掌握并求解此类问题．
∴AE=
AD，CF=BC，∵四边形ABCD是平行四边形，
∴AD∥BC，∴AE∥CF，AE=CF，
∴四边形AFCE是平行四边形，
∴AF∥CE，
同理可证：BE∥DF，
∴四边形GFHE是平行四边形，
∴EF与GH互相平分．
分析：可先求解四边形AFCE是平行四边形，进而利用平行四边形的性质得出四边形GFHE是平行四边形，即可得出结论．
点评：本题主要考查平行四边形的判定问题，能够熟练掌握并求解此类问题．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
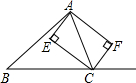已知：如图，CE、CF分别是△ABC的内外角平分线，过点A作CE、CF的垂线，垂足分别为E、F．
21、已知：如图，E，F分别是平行四边形ABCD的边AD，BC的中点．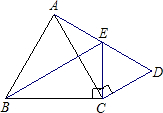
已知：如图，△BCE、△ACD分别是以BE、AD为斜边的直角三角形，且BE=AD，△CDE是等边三角形．求证：△ABC是等边三角形．
已知：如图，E，F分别是?ABCD的边AD，BC的中点．求证：AF=CE．
已知，如图，BE、CF分别是△ABC的边AC、AB上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．请你判断线段AD与AG有什么关系？并证明．