Question

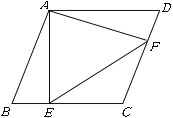
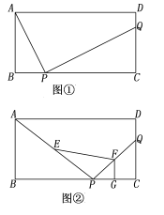
【题目】已知：如图①，②，在矩形ABCD中，AB=4，BC=8，P，Q分别是边BC，CD上的点．

(1)如图①，若AP⊥PQ，BP=2，求CQ的长；

(2)如图②，若=2，且E，F，G分别为AP，PQ，PC的中点，求四边形EPGF的面积．

Answer 1

【答案】(1)CQ=3；(2)S四边形EPGF=4.

【解析】

（1）易证△ABP∽△PCQ，根据对应线段成比例即可求出CQ；

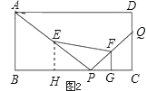
（2）取BP的中点H，连结，由三角形的中位线的性质可得四边形是直角梯形，由=2，设CQ=a，则BP=2a，用含a的代数式表示出EH,FG,HP,HG，用梯形和三角形的面积公式求得的值即可.

解：(1)由△ABP∽△PCQ．

∴．

(2)取BP的中点H，连结，由=2，

设CQ=a，则BP=2a，

∵E，F，G，H分别为AP，PQ，PC，BP的中点，

∴ ， ，

又∵ ，，

∴ ，．

∴四边形是直角梯形．

∴，

， ．

∴S梯形EHGF===4+a，

S△EHP===a．

∴．