题目内容
某商场为了吸引顾客,设计了一个摸球获奖的箱子,箱子中共有20个球,其中红球2个,兰球3个,黄球5个,白球10个,并规定购买100元的商品,就有一次摸球的机会,摸到红、兰、黄、白球的(一次只能摸一个),顾客就可以分别得到80元、30元、10元、0元购物卷,凭购物卷仍然可以在商场购买,如果顾客不愿意摸球,那么可以直接获得购物卷10元.
(1)每摸一次球所获购物卷金额的平均值是多少?
(2)你若在此商场购买100元的货物,两种方式中你应选择哪种方式?为什么?
(1)证明:连接OE,
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO, ∠DAO=∠DEO=90°, ……………………2分
 ∴∠AOD=∠EOD=
∴∠AOD=∠EOD=![]() ∠AOE,
∠AOE,
∵∠ABE=![]() ∠AOE
∠AOE
∴∠AOD=∠ABE,
∴OD∥BE …………………5分
(2)由(1)得:∠AOD=∠EOD=![]() ∠AOE,
∠AOE,
同理,有:∠BOC=∠EOC=![]() ∠BOE
∠BOE
∴∠AOD+∠EOD+∠BOC+∠EOC=180°
∴∠EOD+∠EOC=90°,
∴△DOC是直角三角形,…………………………7分
∴ CD=![]() ……………………9分
……………………9分

练习册系列答案
相关题目
 21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
21、某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.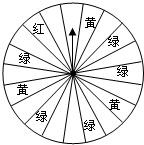 某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少?
某商场为了吸引顾客,设立了一个可以自由转动的转盘.并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得100元、50元、20元购物券(转盘被等分成20个扇形),甲顾客购物120元,他获得购物卷的概率是多少?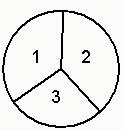 指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券.
指针所指数字之和为奇数,顾客可获得两次数字之和的9倍的购物券,④其余情况无奖;若顾客不愿转动转盘,可直接获得30元购物券. 某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为
某商场为了吸引顾客,设立一个转盘,如图所示,转盘被平分为16份.规定:当顾客每购买500元金额商品时,就能获得一次转动机会,如果转盘的指针正好对准红、黄、蓝区域,可分别获得100元,50元,20元的购物券,甲顾客购物530元,他获得购物券的概率为