题目内容
已知:直线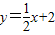 分别与x轴、y轴交于点A、点B,点P(a,b)在直线AB上,点P关于y轴的对称点P′在反比例函数
分别与x轴、y轴交于点A、点B,点P(a,b)在直线AB上,点P关于y轴的对称点P′在反比例函数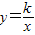 图象上.
图象上.(1)当a=1时,求反比例函数
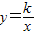 的解析式;
的解析式;(2)设直线AB与线段P′O的交点为C.当P′C=2CO时,求b的值;
(3)过点A作AD∥y轴交反比例函数图象于点D,若AD=
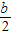 ,求△P′DO的面积.
,求△P′DO的面积.
【答案】分析:(1)根据点P在直线AB上,a=1时,得出b的值,即可得出P点坐标,进而得出P′坐标,求出反比例函数解析式即可;
(2)连接PP′,证出△PP'C∽△OCA,利用P′C=2CO,得出PP′=2OA,进而求出A,B两点坐标得出a,b的值即可;
(3)分别根据当点P在第一象限时,以及当点P在第二象限时,求出D,P′坐标,求出△P′DO的面积即可.
解答: 解:(1)如图1,∵点P在直线AB上,a=1时,b=
解:(1)如图1,∵点P在直线AB上,a=1时,b= ×1+2=
×1+2= ,
,
∴P(1, ),
),
∴P′(-1, ),代入
),代入 得
得 ,
,
∴ ,
,
(2)如图1,连接PP′,
∵点P和点P'关于y轴对称
∴PP′∥x轴
∴△PP'C∽△AOC,
∴PP′:OA=P′C:CO,
∵P′C=2CO,
∴PP′=2OA
∵ 与x轴交于点A、与y轴交于点B,
与x轴交于点A、与y轴交于点B,
∴A(-4,0),B(0,2)可得OA=4,
∴PP'=8,P和P’关于Y轴对称,
∴a=4,
∴b= ×4+2=4;
×4+2=4;
(3)如图2,当点P在第一象限时:
∵点P和点P'关于y轴对称且P(a,b),
∴P'(-a,b),
∵AD∥y,
∴D(-4, ),
),
∵点P'、点D在 上,
上,
∴-4× =-a×b,
=-a×b,
∴a=2,
∴b= ×2+2=3,
×2+2=3,
∵D(-4, ),P'(-2,3)
),P'(-2,3)
∴ ,
,
如图3,当点P在第二象限时:D(-4,- ),
),
∴-4×(- )=-a×b,
)=-a×b,
∴a=-2,
∴b= ×(-2)+2=1,
×(-2)+2=1,
∵D(-4,- ),P'(2,1),
),P'(2,1),
故直线DP′的解析式为;y= x+
x+ ,
,
则OE= ,
,
S△P′OD=S△P′EO+S△DEO= ×
× ×2+
×2+ ×
× ×4=
×4= .
.
综上:S△P′OD= 或
或 .
.
点评:此题主要考查了反比例函数的综合应用以及三角形面积求法等知识,根据数形结合,分类讨论得出P点位置是解题关键.
(2)连接PP′,证出△PP'C∽△OCA,利用P′C=2CO,得出PP′=2OA,进而求出A,B两点坐标得出a,b的值即可;
(3)分别根据当点P在第一象限时,以及当点P在第二象限时,求出D,P′坐标,求出△P′DO的面积即可.
解答:
 解:(1)如图1,∵点P在直线AB上,a=1时,b=
解:(1)如图1,∵点P在直线AB上,a=1时,b= ×1+2=
×1+2= ,
,∴P(1,
 ),
),∴P′(-1,
 ),代入
),代入 得
得 ,
,∴
 ,
,(2)如图1,连接PP′,
∵点P和点P'关于y轴对称
∴PP′∥x轴
∴△PP'C∽△AOC,
∴PP′:OA=P′C:CO,
∵P′C=2CO,
∴PP′=2OA
∵
 与x轴交于点A、与y轴交于点B,
与x轴交于点A、与y轴交于点B,∴A(-4,0),B(0,2)可得OA=4,
∴PP'=8,P和P’关于Y轴对称,
∴a=4,
∴b=
 ×4+2=4;
×4+2=4;(3)如图2,当点P在第一象限时:
∵点P和点P'关于y轴对称且P(a,b),

∴P'(-a,b),
∵AD∥y,
∴D(-4,
 ),
),∵点P'、点D在
 上,
上,∴-4×
 =-a×b,
=-a×b,∴a=2,
∴b=
 ×2+2=3,
×2+2=3,∵D(-4,
 ),P'(-2,3)
),P'(-2,3)∴
 ,
,
如图3,当点P在第二象限时:D(-4,-
 ),
),∴-4×(-
 )=-a×b,
)=-a×b,∴a=-2,
∴b=
 ×(-2)+2=1,
×(-2)+2=1,∵D(-4,-
 ),P'(2,1),
),P'(2,1),故直线DP′的解析式为;y=
 x+
x+ ,
,则OE=
 ,
,S△P′OD=S△P′EO+S△DEO=
 ×
× ×2+
×2+ ×
× ×4=
×4= .
.综上:S△P′OD=
 或
或 .
.点评:此题主要考查了反比例函数的综合应用以及三角形面积求法等知识,根据数形结合,分类讨论得出P点位置是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
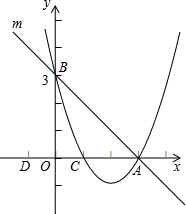 (2013•澄江县二模)如图,已知:直线m分别与x轴、y轴相交于A、B两点,抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.
(2013•澄江县二模)如图,已知:直线m分别与x轴、y轴相交于A、B两点,抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.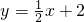 分别与x轴、y轴交于点A、点B,点P(a,b)在直线AB上
分别与x轴、y轴交于点A、点B,点P(a,b)在直线AB上 ,点P关于y轴的对称点P′在反比例函数
,点P关于y轴的对称点P′在反比例函数 图象上.
图象上. ,求△P′DO的面积.
,求△P′DO的面积.
 分别与 x轴、y轴交于点A、点B,点P(
分别与 x轴、y轴交于点A、点B,点P( ,b)在直线AB 上,点P关于
,b)在直线AB 上,点P关于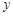 轴的对称点P′ 在反比例函数
轴的对称点P′ 在反比例函数 图象上.
图象上.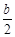 ,求△P’DO的面积.
,求△P’DO的面积. 