题目内容
【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= . 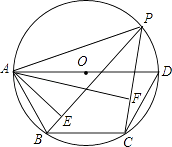
【答案】![]() a
a
【解析】解:如图,连接OB、OC.
∵AD是直径,AB=BC=CD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠AOB=∠BOC=∠COD=60°,
∴∠APB= ![]() ∠AOB=30°,∠APC=
∠AOB=30°,∠APC= ![]() ∠AOC=60°,
∠AOC=60°,
在Rt△APE中,∵∠AEP=90°,
∴AE=APsin30°= ![]() a,
a,
在Rt△APF中,∵∠AFP=90°,
∴AF=APsin60°= ![]() a,
a,
∴AE+AF= ![]() a.
a.
所以答案是 ![]() a.
a.
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目