题目内容
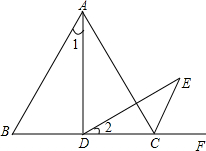 如图,△ABC是等边三角形,点D是边BC上(除B、C外)的任意一点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E
如图,△ABC是等边三角形,点D是边BC上(除B、C外)的任意一点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E
(1)求证:∠1=∠2;
(2)求证:AD=DE.
 证明:(1)∵△ABC是等边三角形,∠ADE=60°
证明:(1)∵△ABC是等边三角形,∠ADE=60°∴∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
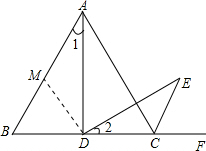
(2)如图,在AB上取一点M,使BM=BD,连接MD.
∵△ABC是等边三角形
∴∠B=60°
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是△ABC外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE,
∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中
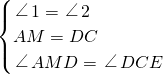 ,
,∴△AMD≌△DCE(ASA).
∴AD=DE.
分析:(1)根据等边三角形的性质得出,∠ADE=60°,再利用外角的性质得出,∠ADC=∠2+∠ADE=∠1+∠B,进而得出∠1=∠2;
(2)根据(1)中的结论,以及角平分线的性质得出∠AMD=∠DCE,进而得出△AMD≌△DCE即可得出答案.
点评:此题主要考查了等边三角形的性质以及全等三角形的判定,得出MA=CD是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
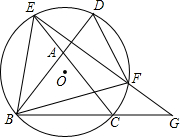 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.