题目内容
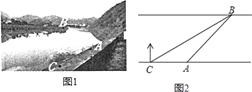
【题目】如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60m到达C点，测得点B在点C的北偏东60°方向，如图2．
（1）求∠CBA的度数．
（2）求出这段河的宽（结果保留根号）．
【答案】（1）∠CBA =15°；（2）
【解析】试题分析：（1）根据三角形的外角的性质、结合题意计算即可；（2）作BD⊥CA交CA的延长线于D，设BD=xm，根据正切的定义用x表示出CD、AD，根据题意列出方程，解方程即可
试题解析：（1）由题意得，∠BAD=45°，∠BCA=30°， ∴∠CBA=∠BAD﹣∠BCA=15°；
（2）作BD⊥CA交CA的延长线于D， 设BD=xm， ∵∠BCA=30°， ∴CD=
=
x，
∵∠BAD=45°， ∴AD=BD=x， 则
x﹣x=60， 解得x=
≈82，
答：这段河的宽约为82m．
练习册系列答案
相关题目
【题目】某学校在开展“节约每一滴水”的活动中，从七年级的100名同学中选出20名同学汇报了各自家庭一个月的节水情况，将有关数据（每人上报节水量都是正整数）整理如下表：
节水量x/t | 0.5≤x＜1.5 | 1.5≤x＜2.5 | 2.5≤x＜3.5 | 3.5≤x＜4.5 |
人数 | 6 | 4 | 8 | 2 |
请你估计这100名同学的家庭一个月节约用水的总量大约是（ ）
A.180tB.300tC.230tD.250t
