题目内容
【题目】如图1，在
中，
，
，分别过
、
两点作过点
的直线
的垂线，垂足为
、
；
（1）如图1，当、两点在直线
的同侧时，猜想，
、
、
三条线段有怎样的数量关系？并说明理由.
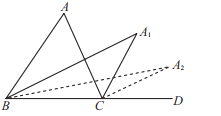
（2）如图2，当、两点在直线的两侧时，、、三条线段有怎样的数量关系？并说明理由.
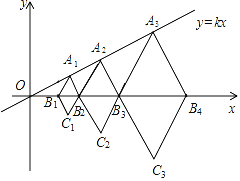
（3）如图3，，
，
.点
从点出发沿
路径向终点运动；点
从点出发沿
路径向终点运动.点和分别以每秒2和3个单位的速度同时开始运动，只要有一点到达相应的终点时两点同时停止运动；在运动过程中，分别过和作
于
，
于
.问：点运动多少秒时，
与
全等？（直接写出结果即可）
【答案】（1）
（2）
（3）当
点运动6秒或10秒时
与
全等
【解析】
（1）根据题意首先证明
，在采用等量替换即可证明.
（2）根据题意首先证明
，在采用等量替换即可证明
.
（3）根据与全等，列方程即可，注意要分类讨论.
（1）.理由如下：
∵在
中，
，
∴
，
又∵
，
∴
，
∴
，
∵
，
∴，
∴
，
，
∴
.
（2）..理由如下：
∵
，
，
∴，
∴
，
∵，
∴，
∴
，
在
和
中，
∵
，
，，
∴，
∴，，
∵
，
∴
，
∴；
（3）解：①当点在
上，点
在
上时，
，
解得
，
②当点在上，点在上时，
，
解得
.
③当点在上，点在上时，（t>11）
解得：t=6(舍)
④当点运动到
点，点在上时，（11<t≤
）
，
解得
（舍）.
所以当点运动6秒或10秒时与全等.
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
