题目内容
如图,抛物线与x轴相交于B,C两点,与y轴相交于点A,P(2a,-4a2+7a+2)(a是实数)在抛物线上,直线y=k x +b经过A,B两点.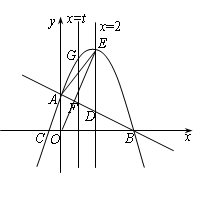
(1)求直线AB的解析式;
(2)平行于y轴的直线x=2交直线AB于点D,交抛物线于点E.
①直线x=t(0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
②将抛物线向上平移m(m>0)个单位,当EO平分∠AED时,求m的值.
(1) (2)①t1=1,t2="3" ②
(2)①t1=1,t2="3" ②
解析试题分析:(1)∵P(2a,-4a2+7a+2)(a是实数)在抛物线上,
∴抛物线的解析式为y=-4a2+7a+2=-4×( )2+7×
)2+7× +2=-x2+
+2=-x2+ x+2.
x+2.
当y=0时,即-x2+ x+2=0,解得x1=-
x+2=0,解得x1=- ,x2=4.
,x2=4.
当x=0时,y=2.
∴A(0,2),B(4,0),C(- ,0).
,0).
∴ 解得
解得
故直线AB的解析式为y=- x+2.
x+2.
(2)①∵点E(2,5),D(2,1),G(t,- t2+ t+2),F(t,-
t+2),F(t,- t+2),
t+2),
∴DE=4,FG=-t2+ t+2-(-
t+2-(- t+2)=-t2+4t.
t+2)=-t2+4t.
∵FG∶DE=3∶4,
∴-t2+4t=3.
解得t1=1,t2=3.
②设点A(0,2+m),则点E(2,5+m)
作AH⊥DE,垂足为H.
∴AE2=AH2+HE2=22+(5+m-2-m)2=13.即AE= .
.
∵EO平分∠AED,∴∠AEO=∠DEO.
∵AO∥ED,∴∠DEO=∠AOE.
∴∠AEO=∠AOE.
∴AO=AE,即2+m= .解得m=2-
.解得m=2-
考点:函数与几何图形的结合
点评:该题主要考查学生利用待定系数法求一次函数解析式以及分析二次函数在坐标系中的几何意义,是常考题。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 如图,已知A(5,-4),⊙A与x轴分别相交于点B、C,⊙A与y轴相且于点D,
如图,已知A(5,-4),⊙A与x轴分别相交于点B、C,⊙A与y轴相且于点D,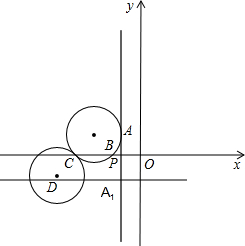 A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P
A(A在第二象限),点A关于x轴的对称点是A1,直线AA1与x轴相交点P 已知:如图,抛物线y=x2+bx+c与x轴的一个相交点坐标为A(1,0),与y轴上的交点坐标C(0,3).
已知:如图,抛物线y=x2+bx+c与x轴的一个相交点坐标为A(1,0),与y轴上的交点坐标C(0,3). (2012•相城区一模)如图,抛物线y=
(2012•相城区一模)如图,抛物线y= 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴相交点C(0,
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,0)两点,与y轴相交点C(0,