题目内容
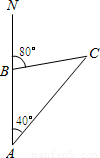
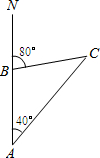 如图,轮船以每小时20海里的速度向正北方向航行,测得灯塔C在北偏东40°的方向(即∠NAC=40°),半小时后,轮船航行到B处,测得灯塔C在北偏东80°的方向(即∠NBC=80°),这时轮船在B处与灯塔C的距离是________海里.
如图,轮船以每小时20海里的速度向正北方向航行,测得灯塔C在北偏东40°的方向(即∠NAC=40°),半小时后,轮船航行到B处,测得灯塔C在北偏东80°的方向(即∠NBC=80°),这时轮船在B处与灯塔C的距离是________海里.
10
分析:根据已知条件和“三角形的外角是与其不相邻的内角和”求出∠C,关键是利用角与角的关系求得AB=BC,再利用路程公式求得AB的长即可.
解答:∵∠NAC=40°,NBC=80°,
∴∠C=∠NBC-∠NAC=80°-40°=40°,
∴∠C=∠NAC=40°,
∴BC=BA.
∵BC=20× =10(海里),
=10(海里),
∴BC=BA=10(海里).
答:B处到灯塔C处的距离为10海里.
故答案为:10.
点评:本题主要考查了等腰三角形判定与性质,关键是根据已知条件求得角的度数及准确理解AB即是路程,是一道基础题,比较容易.
分析:根据已知条件和“三角形的外角是与其不相邻的内角和”求出∠C,关键是利用角与角的关系求得AB=BC,再利用路程公式求得AB的长即可.
解答:∵∠NAC=40°,NBC=80°,
∴∠C=∠NBC-∠NAC=80°-40°=40°,
∴∠C=∠NAC=40°,
∴BC=BA.
∵BC=20×
 =10(海里),
=10(海里),∴BC=BA=10(海里).
答:B处到灯塔C处的距离为10海里.
故答案为:10.
点评:本题主要考查了等腰三角形判定与性质,关键是根据已知条件求得角的度数及准确理解AB即是路程,是一道基础题,比较容易.

练习册系列答案
相关题目
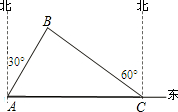 如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,
如图,一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,上午12时行到C处,测得灯塔恰好在它的北偏西60°,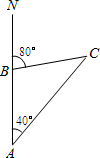 如图,轮船以每小时20海里的速度向正北方向航行,测得灯塔C在北偏东40°的方向(即∠NAC=40°),半小时后,轮船航行到B处,测得灯塔C在北偏东80°的方向(即∠NBC=80°),这时轮船在B处与灯塔C的距离是
如图,轮船以每小时20海里的速度向正北方向航行,测得灯塔C在北偏东40°的方向(即∠NAC=40°),半小时后,轮船航行到B处,测得灯塔C在北偏东80°的方向(即∠NBC=80°),这时轮船在B处与灯塔C的距离是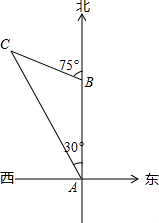 如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据:
如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处.轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处.当该轮船继续 航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的大致距离.(结果精确到0.1海里,参考数据: