题目内容
【题目】已知点A（2，﹣3）在双曲线y＝
上，则下列哪个点也在此双曲线上（ ）
A. （1，6） B. （﹣1，6） C. （2，3） D. （﹣2，﹣3）
【答案】B
【解析】
求得k的值，然后由给点的横纵坐标相乘，结果是﹣6的，就在此函数图象上．
∵A（2，﹣3）在双曲线y＝
上，
∴k＝xy＝（﹣2）×3＝﹣6，
∴只需把各点横纵坐标相乘，结果为﹣6的点在函数图象上．
A、因为1×6＝6≠k，所以该点不在双曲线y＝上．故A选项错误；
B、因为﹣1×6＝﹣6＝k，所以该点在双曲线y＝上．故B选项正确；
C、因为2×3＝6≠k，所以该点不在双曲线y＝上．故C选项错误；
D、因为﹣2×（﹣3）＝6≠k，所以该点不在双曲线y＝上．故D选项错误．
故选B．
举一反三期末百分冲刺卷系列答案【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
时间（第x天） | 1 | 3 | 6 | 10 | … |
日销售量（m件） | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
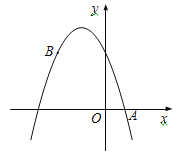
【题目】如图，已知二次函数y＝ax2＋bx＋3的图像经过点A（1，0），B（－2，3）．
（1）求该二次函数的表达式；
（2）求该二次函数的最大值；
（3）结合图像，解答问题：当y＞3时，x的取值范围是 ．
【题目】抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
（1）根据上表填空：
①抛物线与x轴的交点坐标是_________和_________；
②抛物线经过点（-3，_________）；
（2）试确定抛物线y=ax2+bx+c的解析式.
