题目内容
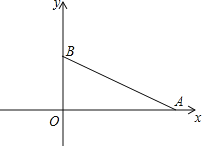
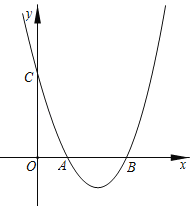
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点 C.
(1)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(2)在(1)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
【答案】(1)y=x2﹣4x+3;(2)3![]() .
.
【解析】
(1)先根据等腰直角三角形的腰长求出OB=OC=3,进而求出点B,C坐标,最后用待定系数法即可得出结论;
(2)先确定出抛物线的对称轴,进而求出点C'的坐标,找出PA+PC的最小值为AC',再求出点A坐标,即可得出结论.
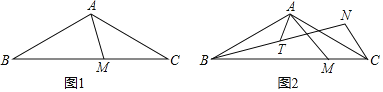
(1)如图1,连接BC,

∵△OBC是等腰直角三角形,∠BOC=90°,
∴OB=OC,
∵腰长为3,
∴OB=OC=3,
∴B(3,0),C(0,3),
将点B(3,0),C(0,3)代入抛物线解析式y=x2+mx+n中,得,![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3;
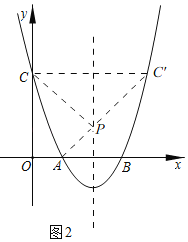
(2)如图2,由(1)知,抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴直线为x=2,
∵点C(0,3),
∴点C关于抛物线的对称轴x=2的对称点C'(4,3),
连接AC'交抛物线的对称轴于P,此时,PA+PC的值最小,最小值为AC',
针对于抛物线的解析式为y=x2﹣4x+3,令y=0,则x2﹣4x+3=0,
解得,x=1或x=3,
∴A(1,0),
∵C'(4,3),
∴AC'![]() ,
,
即:PA+PC的最小值为![]() ,
,
故答案为:![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … |
| 0 |
| 1 |
| 2 |
| … |
y | … |
| ﹣1 |
| m |
| ﹣1 | n | … |
则对于该函数的性质的判断:①该二次函数有最大值;②不等式y>﹣1的解集是x<0或x>2;③方程ax2+bx+c=0的两个实数根分别位于﹣![]() <x<0和2<x<
<x<0和2<x<![]() 之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
A.②③B.②④C.①③D.③④