题目内容
已知m2+m-1=0,则m3+2m2+2013= .
考点:因式分解的应用
专题:
分析:先将m2+m-1=0变形为m2+m=1.再提取公因式m,将m2+m作为一个整体直接代入计算即可.
解答:解:∵m2+m-1=0,
∴m2+m=1,
∴m3+2m2+2013,
=m(m2+m)+m2+2013,
=m2+m+2013,
=1+2013,
=2014.
故答案为:2014.
∴m2+m=1,
∴m3+2m2+2013,
=m(m2+m)+m2+2013,
=m2+m+2013,
=1+2013,
=2014.
故答案为:2014.
点评:本题考了查因式分解,解决本题的关键是将m2+m作为一个整体直接代入,求得结果.

练习册系列答案
相关题目
下列各图中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
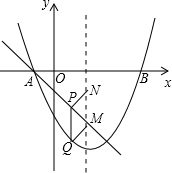 如图,抛物线y=ax2+bx-
如图,抛物线y=ax2+bx-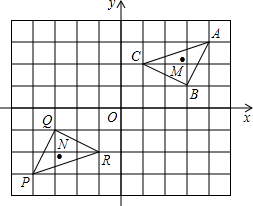 如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下:
如图,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.在这种变换下: