题目内容
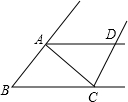
 如图,△ABC≌△ADC,∠BAC=60°,∠ACD=23°,那么∠D=
如图,△ABC≌△ADC,∠BAC=60°,∠ACD=23°,那么∠D=
- A.87°
- B.97°
- C.83°
- D.37°
B
分析:根据全等三角形的性质求出∠DAC的度数,根据三角形的内角和定理得出∠D=180°-∠DAC-∠ACD,代入求出即可.
解答:∵△ABC≌△ADC,∠BAC=60°,
∴∠DAC=∠BAC=60°,
∵∠ACD=23°,
∴∠D=180°-∠DAC-∠ACD=97°,
故选B.
点评:本题考查了三角形的内角和定理和全等三角形的性质,注意:全等三角形的对应边相等,对应角相等.
分析:根据全等三角形的性质求出∠DAC的度数,根据三角形的内角和定理得出∠D=180°-∠DAC-∠ACD,代入求出即可.
解答:∵△ABC≌△ADC,∠BAC=60°,
∴∠DAC=∠BAC=60°,
∵∠ACD=23°,
∴∠D=180°-∠DAC-∠ACD=97°,
故选B.
点评:本题考查了三角形的内角和定理和全等三角形的性质,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
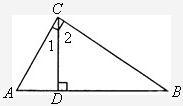
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
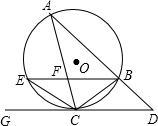
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.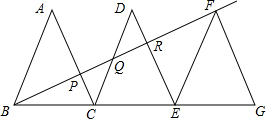 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且