题目内容
11、在1、2、3、…、2007这2007个自然数中有
268
个自然数能同时被2和3整除，而不能被5整除．分析：根据已知条件，现列举出能同时被2和3整除即能被6整除的数6，12，18，24…，再在列举的数中列举出能被5整除的数30，60，90，120，…，然后观察这些数得到两个等差数列．
解答：解：能同时被2和3整除即能被6整除的数在1，2，3，…，2007这2007个自然数中有6，12，18，24，…，1998，得到一个公差是6的等差数列．
设这样的数有n个，则：2004=6+（n-1）×6，得n=334．所以同时被2和3整除的数有334个．
在这334个数中能被5整除的数有30，60，90，120，…，1980，得到一个公差是30的等差数列．设这样的数有m个，则
1980=30+（m-1）×30，得m=66，即能被5整除的数有66个．
所以：能同时被2和3整除，而且不能被5整除的数有334-66=268（个）
故答案为：268．
设这样的数有n个，则：2004=6+（n-1）×6，得n=334．所以同时被2和3整除的数有334个．
在这334个数中能被5整除的数有30，60，90，120，…，1980，得到一个公差是30的等差数列．设这样的数有m个，则
1980=30+（m-1）×30，得m=66，即能被5整除的数有66个．
所以：能同时被2和3整除，而且不能被5整除的数有334-66=268（个）
故答案为：268．
点评：此题主要考查了数的整除性问题，考查学生分析、观察问题的能力．关键是善于发现、总结问题，运用等差数列解题．
练习册系列答案
相关题目
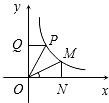设P（a，b），M（c，d）是反比例函数y=
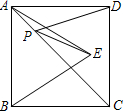如图所示，正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
20、如图，在△ABC中，点D，E分别是AB，AC边的中点，若把△ADE绕着点E顺时针旋转180°得到△CFE．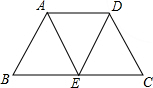
在等腰梯形ABCD中，AD∥BC，E是BC的中点，连接AE，DE，AE与DE相等吗？
