题目内容
如图所示，在△ABC中，
AB=AC，BD⊥AC于点D，CE⊥AB于点E，BD、CE相交于点F.
求证：AF平分∠BAC.
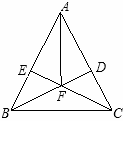
证明：∵ DB⊥AC ，CE⊥AB，∴ ∠AEC=∠ADB=90°.
在△ACE与△ABD中，∵ 
∴ △ACE≌△ABD （AAS）,
∴ AD=AE.
在Rt△AEF与Rt△ADF中，
∵ 
∴ Rt△AEF≌Rt△ADF（HL），
∴ ∠EAF=∠DAF，
∴ AF平分∠BAC.
练习册系列答案
相关题目
题目内容
如图所示，在△ABC中，AB=AC，BD⊥AC于点D，CE⊥AB于点E，BD、CE相交于点F.
求证：AF平分∠BAC.
证明：∵ DB⊥AC ，CE⊥AB，∴ ∠AEC=∠ADB=90°.
在△ACE与△ABD中，∵
∴ △ACE≌△ABD （AAS）,
∴ AD=AE.
在Rt△AEF与Rt△ADF中，
∵
∴ Rt△AEF≌Rt△ADF（HL），
∴ ∠EAF=∠DAF，
∴ AF平分∠BAC.
如图所示，在△ABC中，∠A=47°，∠C=77°，DE∥BC，BF平分∠ABC，BF交DE于点F，求∠BFE的度数．
如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作AF∥BC交ED的延长线于点F，连接AE，CF．
15、如图所示，在△ABC中，DM、EN分别垂直平分AB和AC，交BC于D、E，若∠DAE=50°，则∠BAC=
如图所示，在△ABC中，AB=AC，DE是边AB的垂直平分线，交AB于E，交AC于D，若△BCD的周长为18cm，△ABC的周长为30cm，那么BE的长为
如图所示，在△ABC中，BC=7cm，AB=25cm，AC=24cm，P点在BC上从B点向C点运动（不包括点C），点P的运动速度为2cm∕s；Q点在AC上从C点向点A运动（不包括点A），运动速度为5cm∕s，若点P、Q分别从B、C同时运动，请解答下面的问题，并写出主要过程．