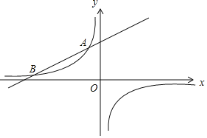
题目内容
【题目】如图所示,已知![]() 点的横坐标为2,将
点的横坐标为2,将![]() 点向右平移2个单位,再向下平移2个单位得到
点向右平移2个单位,再向下平移2个单位得到![]() 点,且
点,且![]() 、
、![]() 两点均在双曲线
两点均在双曲线![]() 上.
上.
(1)求反比例函数的解析式.(2)若直线![]() 于反比例函数
于反比例函数![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】
(1)设A点坐标为(2,m),则点B的坐标为(4,m-2),把两点代入反比例函数中即可求出m,k,即可求解;
(2)根据(1)求出A,B,B’的坐标,再求出直线直线AB’的解析式,得到M的坐标即可求解.
解(1)设A点坐标为(2,m),则点B的坐标为(4,m-2),
∵![]() 、
、![]() 两点均在双曲线
两点均在双曲线![]() 上.
上.
∴![]() ,
,
∴![]() ,
,
∴反比例函数的解析式为![]() ,
,
(2)如图,由(1)得:A(2,4),B(4,2), 由题意可知点![]() 与点
与点![]() 关于原点对称,
关于原点对称,
∴点![]() 坐标为(-4,-2)
坐标为(-4,-2)
设直线![]() 为
为![]() ,将
,将![]() 和
和![]() (-4,-2)代入得
(-4,-2)代入得
![]() ,
,
解得![]() ,
,
∴直线AB’的解析式为![]()
若直线![]() 与y轴交于点M
与y轴交于点M
∴M(0,2),OM=2
∴![]()


练习册系列答案
相关题目