Question

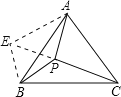
【题目】如图，已知点P是等边△ABC内一点，PA=3，PB=4，PC=5，求∠APB的度数．

（1）在图中画出：将△BPC绕点B逆时针旋转60°后得到△BEA；

（2）连接EP，完成你的解答.

Answer 1

【答案】（1）详见解析；（2）150°．

【解析】

（1）将△BPC绕点B逆时针旋转60°得△BEA，根据旋转的性质画出图形即可；（2）连EP，根据旋转的性质得BE=BP=4，AE=PC=5，∠PBE=60°，则△BPE为等边三角形，得到PE=PB=4，∠BPE=60°，在△AEP中，AE=5，AP=3，PE=4，根据勾股定理的逆定理可得到△APE为直角三角形，且∠APE=90°，即可得到∠APB的度数．

（1）如图：将△BPC绕点B逆时针旋转60°得△BEA；

（2） 连EP，

∴BE=BP=4，AE=PC=5，PBE=60°

∴△BPE为等边三角形，

∴PE=PB=4，∠BPE=60°，

在△AEP中，AE=5，AP=3，PE=4，

∴AE2=PE2+PA2，

∴△APE为直角三角形，且∠APE=90°，

∴∠APB=90°+60°=150°．