题目内容
有一个边长为6cm的正三角形ABC木块，点P是边CA的延长线上的点，在A、P之间拉一条细绳，绳长AP为15cm，握住点P，拉直细绳，把它全部紧紧缠绕在△ABC木块上（缠绕时木块不动）．若圆周率取3.14，则点P运动的路线长为
56.5cm
56.5cm
（精确到0.1cm）分析：根据如图所示可知点P运动的路线就是图中三外扇形的弧长，正三角形ABC的内角为60度，所以第一个小扇形的弧长等于
，第二个为
，第三个为
，将三段弧的长度相加即为所求．
| 120π×15 |
| 180 |
| 120π×9 |
| 180 |
| 120π×3 |
| 180 |
解答：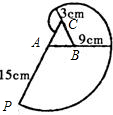
解：第一段弧长=
=10πcm；
第二段弧长=
=6πcm；第三段弧长=
=2πcm；
所以三段弧长=18π=56.5cm．
故答案是：56.5cm．
解：第一段弧长=| 120π×15 |
| 180 |
第二段弧长=
| 120π×9 |
| 180 |
| 120π×3 |
| 180 |
所以三段弧长=18π=56.5cm．
故答案是：56.5cm．
点评：本题的关键是理解点P运动的路线就是图中三外扇形的弧长，然后明确扇形的圆心角是120度，半径分别是15cm，9cm，3cm，求值即可．
练习册系列答案
相关题目
如图，有一个边长为6cm的正三角形ABC木块，点P是边CA的延长线上的点，在A、P之间拉一条细绳，绳长AP为15cm．握住点P，拉直细绳，把它全部紧紧缠绕在△ABC木块上（缠绕时木块不动），若圆周率取3.14，点P运动的路线长为（ ）（精确到0.1cm）| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |
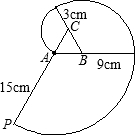如图，有一个边长为6cm的正三角形木块ABC，点P是CA延长线上的一点，在A、P之间拉一条长为15cm细丝，握住点P，拉直细线，把它全部紧紧绕在△ABC木块上（缠绕时木块不动），则点P运动的路线长为（π取3.14，精确到0.1cm）（ ）| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |
10、如图，有一个边长为6cm的正三角形，从它的三个角截去三个小等边三角形后得到一个正六边形，则正六边形的边长为