题目内容
 计算四边形ABCD的面积.
计算四边形ABCD的面积.
分析:根据观察图形可以看出四边形ABCD的面积为△ABD和△BCD的面积之和,根据AD,AB可以计算△ABD的面积和BD的长,根据CD,BD可以计算△BCD的面积,即可解题.
解答:解:在Rt△ABD中,BD为斜边,
AD=12,AB=16,
则BD=
=20,
故四边形ABCD的面积为S△ABD+S△BCD=
×12×16+
×15×20=96+150=246.
答:四边形ABCD的面积为246.
AD=12,AB=16,
则BD=
| AD2+AB2 |
故四边形ABCD的面积为S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
答:四边形ABCD的面积为246.
点评:本题考查了勾股定理在直角三角形中的运用,考查了直角三角形面积计算方法,本题中正确的计算△ABD和△BCD的面积是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
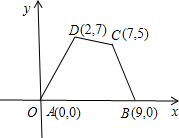 D(2,7).
D(2,7). 如图,在△ABC中,AB=2
如图,在△ABC中,AB=2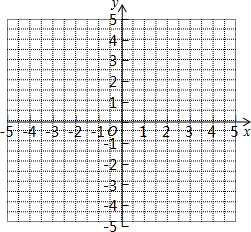 在平面直角坐标系中描出以下各点:A(-2,0)、B(-1,3)、C(2,2)、D(2,-1).
在平面直角坐标系中描出以下各点:A(-2,0)、B(-1,3)、C(2,2)、D(2,-1).