题目内容
已知一次函数y=kx+b(k≠0)和反比例函数y=| k | 2x |
(1)求两个函数的解析式;
(2)若点B是x轴上一点,且△AOB是直角三角形,求B点的坐标.
分析:(1)利用待定系数法把点A(1,1)代入反比例函数关系式可得到k的值,再代入一次函数解析式可得到b的值.
(2)△AOB是直角三角形,分两种情况:①当AB⊥x②当OA⊥AB分别计算.
(2)△AOB是直角三角形,分两种情况:①当AB⊥x②当OA⊥AB分别计算.
解答: 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=
的图象过点A(1,1),
∴k=2,
∴反比例函数关系式是:y=
=
,
一次函数y=kx+b=2x+b,
∵一次函数y=2x+b过点A(1,1),
∴1=2+b,
b=-1,
∴一次函数解析式是:y=2x-1;
(2)①当AB⊥x轴时:OB=AB=1,
∴B(1,0)
②当OA⊥AB′时:OB′=2OB=2,
∴B′(2,0).
∴B点坐标为:(1,0),(2,0).
 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=| k |
| 2x |
∴k=2,
∴反比例函数关系式是:y=
| 2 |
| 2x |
| 1 |
| x |
一次函数y=kx+b=2x+b,
∵一次函数y=2x+b过点A(1,1),
∴1=2+b,
b=-1,
∴一次函数解析式是:y=2x-1;
(2)①当AB⊥x轴时:OB=AB=1,
∴B(1,0)
②当OA⊥AB′时:OB′=2OB=2,
∴B′(2,0).
∴B点坐标为:(1,0),(2,0).
点评:此题主要考查了待定系数法求函数解析式,解决此题的难点是△AOB是直角三角形,分两种情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.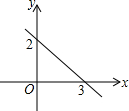 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.