题目内容

如果直角三角形的两直角边分别为3，4，那么它的内切圆的半径为

A.
1
B.
$数学公式$
C.
2 $数学公式$
D.
3 $数学公式$

A
分析：根据勾股定理，得直角三角形的斜边是5．再根据切线长定理可以证明“直角三角形内切圆的半径是直角三角形的两条直角边的和与斜边的差的一半”，所以（3+4-5）÷2=1．
解答：∵直角三角形的两直角边分别为3，4，
∴直角三角形的斜边是5，
∴内切圆的半径为（3+4-5）÷2=1．
故选A．
点评：注意：直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半．

练习册系列答案

海东青中考总复习系列答案

学成教育系统总复习系列答案

全优学习系列答案

名师作业本同步课堂系列答案

毕业总复习全解系列答案

互动课堂教材解读系列答案

小学生奥数点拨系列答案

世纪天成中考专家系列答案

小升初名师帮你总复习系列答案

成长阅读系列答案

相关题目

12、下列说法正确的是（　　）

A、若Rt△ABC≌Rt△DEF，且△ABC的两条直角边分别是水平和竖直状态，那么△DEF的两条直角边也一定分别是水平和竖直状态

B、如果△ABC≌△DEF，△DEF≌△GHK，那么△ABC≌△GHK

C、有一条公共边，而且公共边在每个三角形中都是腰的两个等腰三角形一定全等

D、有一条相等的边，而且相等的边在每个三角形中都是底边的两个等腰三角形全等

根据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连接得到一个直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括为“勾三、股四、弦五”．
（1）观察：①3，4，5；②5，12，13；③7，24，25；…发现这些勾股数的勾都是奇数，且从3起就没有间断过，并且

（25-1）=12，

（25+1）=13
发现规律：勾为n（n≥3，且n为奇数）时有：股=

（n²-1），弦=

（n²+1）分别写出能表示7，24，25的股和弦的算式？
（2）根据（1）的规律，用n（n为奇数，且n≥3）的代数式来表示所有这些勾股数的勾，股，弦，合理猜想它们之间的两种等量关系并对其中一种猜想加以证明？
（3）继续观察①4，3，5；②6，8，10；②8，15，17；…可以发现各组的第一个数都是偶数，且从4起也没有间断过，运用类似上述的探索的方法，直接用m（m为偶数，且m≥4）的代数式来表示它们的股和弦．

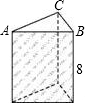如图，是一个直三棱柱的模型，其底面是两直角边长分别为3cm、4cm的直角三角形，侧棱长都是8cm．
（1）设这个直棱柱的面数为f，棱数为e，顶点数为v，求f+v-e的值；
（2）如果将这个直棱柱用铁丝扎出来，至少需要多少长的铁丝？（不计接头长度）
（3）给你一张长15cm，宽8cm的长方形纸片，能否糊出这个三棱柱模型？请通过计算说明．

下列命题的逆命题正确的是（　　）
①如果三角形的一个外角与和它相邻的一个内角相等，那么此三角形是直角三角形．
②在三角形中，如果两边的平方和等于第三边的平方，那么此三角形是直三角形．
③在三角形中，如果两个内角的和等于第三个内角，那么此三角形是直角三角形．

某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：
定义：如果一个正方形的四个顶点都在一个三角形的边上，那么我们就把这个正方形叫做三角形的内接正方形.
结论：在探讨过程中，有三位同学得出如下结果：
甲同学：在钝角、直角、不等边锐角三角形中分别存在____个、________个、________个大小不同的内接正方形.
乙同学：在直角三角形中，两个顶点都在斜边上的内接正方形的面积较大.
丙同学：在不等边锐角三角形中，两个顶点都在较大边上的内接正方形的面积反而较小.
任务：（1）填充甲同学结论中的数据；
（2）乙同学的结果正确吗？若不正确，请举出一个反例并通过计算给予说明，若正确，请给出证明；
（3）请你结合（2）的判定，推测丙同学的结论是否正确，并证明
（如图，设锐角△ABC的三条边分别为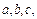不妨设，三条边上的对应高分别为，内接正方形的边长分别为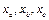.若你对本小题证明有困难，可直接用“”这个结论，但在证明正确的情况下扣1分）.