��Ŀ����
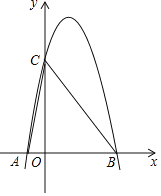
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���䶥��ΪP������PA��AC��CP������C��y��Ĵ���l����֪����P������Ϊ��-3��-4�����߶�PC֮��Ϊ3
��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���䶥��ΪP������PA��AC��CP������C��y��Ĵ���l����֪����P������Ϊ��-3��-4�����߶�PC֮��Ϊ3![]()
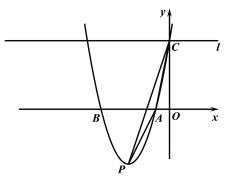
(1)����κ�������ʽ��
(2)MΪֱ��l��һ�㣬����M,C,OΪ���������������A,C,OΪ��������������ƣ���ֱ��д����M�����ꡣ
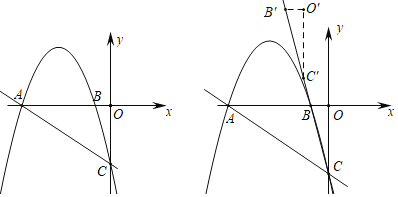
(3)ֱ��l���Ƿ���ڵ�D��ʹ��PBD�����������PAC�������3���������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�� ![]() ����2��
����2��![]() ��(3) ���ڣ�
��(3) ���ڣ�![]()
��������
��1�����ù��ɶ������C�����꣬Ȼ�������߽���ʽд�ɶ���ʽ���ٻ�Ϊһ��ʽ����2�����A,B��������꣬���������֪��ACO�͡�MCO��Ϊֱ��������
��Ȼ�����������������������������г�����ʽ���Ӷ���⣨3������ϵ������ֱ��PC�Ľ���ʽΪy=3x+5����ֱ�߽�x����E����E��![]() ��0������ֱ��PQ��x����F����BD=3AFʱ����PBD�����������PAC�������3�������������ηֱ���⼴�ɽ�����⣮
��0������ֱ��PQ��x����F����BD=3AFʱ����PBD�����������PAC�������3�������������ηֱ���⼴�ɽ�����⣮
�⣺��1������P��PH��y��
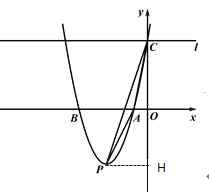
������P��������-3��-4��
��PH=3��OH=4
��OC=x
��Rt��PCH��![]()
��![]()
��ã�![]() ����ֵ��ȥ��
����ֵ��ȥ��
����C��������0,5��
�躯������ʽ![]()
����0,5�����룬![]()
��ã�a=1
�ຯ������ʽΪ![]()
��2����![]() �У���y=0ʱ
�У���y=0ʱ
![]()
��ã�![]()
����A��-1,0����B(-5,0)
��M��ֱ��l��
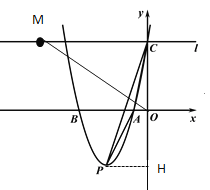
�������֪��ACO�͡�MCO��Ϊֱ��������
��M��x,5��
�൱![]() ʱ����������������
ʱ����������������
��![]()
��ã�![]()
��![]() ʱ����������������
ʱ����������������
��![]()
��ã�![]()
���M������Ϊ![]() ��
��![]() ��
��![]() ��
��![]()
��3����ֱ��PC�Ľ���ʽΪy=kx+b��
����![]()
���![]()
��ֱ��PC�Ľ���ʽy=3x+5��
��ֱ�߽�x����E����E��![]() ��0����
��0����
��ֱ��PD��x����F����BF=3AEʱ����PBD�����������PAC�������3����
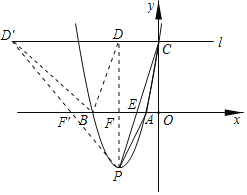
��A(-1,0)��B(-5,0)
��AE=![]() ��
��
��BF=2
��F��-3��0����F'��-7��0��
��F��-3��0��ʱ��ֱ��PF��ֱ��x�ᣬ
��D��-3��5��
��F'��-7��0��ʱ��ֱ��PF'�Ľ���ʽΪy=-x-7��
��D'��-12��5����
�������������������ĵ�D��-3��5����D'��-12��5����