Question

（8分） 一元二次方程的二根（）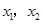
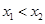是抛物线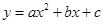与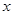轴的两个交点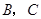的横坐标，
且此抛物线过点．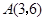
【小题1】（1）求此二次函数的解析式．
【小题2】（2）用配方法求此抛物线的顶点为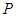 .对称轴
【小题3】（3）当x取什么值时， y随x增大而减小？

Answer 1

【小题1】y=(x+1)-2  
【小题2】∴它的顶点坐标为（-1，-2）对称轴为 直线。
【小题3】当时，即……(x+3)(x-1)=0
解得，=1…
∴x＜-3时…当x取什么值时， y随x增大而减小…………………………………8分

解析考点：抛物线与x轴的交点；二次函数的性质．
分析：（1）先根据题意求出一元二次方程x²+2x-3=0的二根x₁，x₂，把x₁，x₂及A（3，6）分别代入二次函数的解析式．求出a，b，c的值；
（2）用配方法求此抛物线的顶点P的坐标；
（3）根据二次函数的性质判断出为减函数时x的取值范围．
解：（1）一元二次方程x²+2x-3=0可化为（x+3）（x-1）=0，
解得x₁=-3，x₂=1，即抛物线y=ax²+bx+c与x轴的两个交点分别为B（-3，0），C（1，0），
∵抛物线过点A（3，6），
∴把A，B，C三点分别代入抛物线y=ax²+bx+c得，，
解得，
∴此二次函数的解析式为y=x²+x-；
（2）y=x²+x-
=（x²+2x-3）
= [（x²+2x+1）-4]
=（x+1）²-2
故此抛物线的顶点为P（-1，-2）；
（3）∵抛物线的对称轴为x=-1，a=＞0，
∴抛物线开口向上，x＜-1时，y随x增大而减小．