题目内容
如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B(3,0),则由图象可知,不等式ax2+bx+c>0的解集是 .
【答案】分析:由抛物线与x轴的一个交点(3,0)和对称轴x=1可以确定另一交点坐标为(-1,0),又y=ax2+bx+c>0时,图象在x轴上方,由此可以求出x的取值范围.
解答:解:∵抛物线与x轴的一个交点(3,0)
而对称轴x=1
∴抛物线与x轴的另一交点(-1,0)
当y=ax2+bx+c>0时,图象在x轴上方
此时x<-1或x>3
故填空答案:x<-1或x>3.
点评:解答此题的关键是求出图象与x轴的交点,然后由图象找出当y>0时,自变量x的范围,本题锻炼了学生数形结合的思想方法.
解答:解:∵抛物线与x轴的一个交点(3,0)
而对称轴x=1
∴抛物线与x轴的另一交点(-1,0)
当y=ax2+bx+c>0时,图象在x轴上方
此时x<-1或x>3
故填空答案:x<-1或x>3.
点评:解答此题的关键是求出图象与x轴的交点,然后由图象找出当y>0时,自变量x的范围,本题锻炼了学生数形结合的思想方法.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 坐标为(-2,0).
坐标为(-2,0). 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
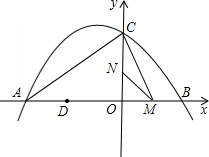
与x轴交于点A、B,点A的坐标为(-2,0). (2013•石景山区二模)如图,抛物线y=-x2+ax+b过点A(-1,0),B(3,0),其对称轴与x轴的交点为C,反比例函数
(2013•石景山区二模)如图,抛物线y=-x2+ax+b过点A(-1,0),B(3,0),其对称轴与x轴的交点为C,反比例函数