题目内容
【题目】如图：在平面直角坐标系xOy中，已知正比例函数y= 
与一次函数y=﹣x+7的图象交于点A．
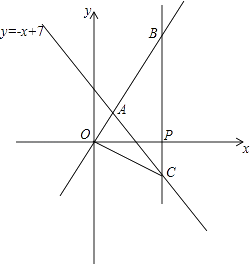
（1）求点A的坐标；
（2）在y轴上确定点M，使得△AOM是等腰三角形，请直接写出点M的坐标；
（3）如图、设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交y= 和y=﹣x+7的图象于点B、C，连接OC，若BC= 
OA，求△ABC的面积及点B、点C的坐标；
（4）在（3）的条件下，设直线y=﹣x+7交x轴于点D，在直线BC上确定点E，使得△ADE的周长最小，请直接写出点E的坐标．
【答案】
（1）解：联立得： 
，
解得： 
，
则点A的坐标为（3，4）
（2）解：根据勾股定理得：OA= 
=5，
如图1所示，分四种情况考虑：
当OM1=OA=5时，M1（0，5）；
当OM2=OA=5时，M2（0，﹣5）；
当AM3=OA=5时，M3（0，8）；
当OM4=AM4时，M4（0， 
），
综上，点M为（0，5）、（0，﹣5）、（0，8）、（0， ）
（3）解：设点B（a， 
a），C（a，﹣a+7），
∵BC= 
OA= ×5=14，
∴ a﹣（﹣a+7）=14，
解得：a=9，
过点A作AQ⊥BC，如图2所示，
∴S△ABC= 
BCAQ= ×14×（9﹣3）=42，
当a=9时， a= ×9=12，﹣a+7=﹣9+7=﹣2，
∴点B（9，12）、C（9，﹣2）
（4）解：如图3所示，作出D关于直线BC的对称点D′，连接AD′，与直线BC交于点E，连接DE，此时△ADE周长最小，
对于直线y=﹣x+7，令y=0，得到x=7，即D（7，0），
由（3）得到直线BC为直线x=9，
∴D′（11，0），
设直线AD′解析式为y=kx+b，
把A与D′坐标代入得： 
，
解得： 
，
∴直线AD′解析式为y=﹣ x+ 
，
令x=9，得到y=1，
则此时点E坐标为（9，1）
【解析】（1）联立正比例函数和一次函数解析式建立方程组，解方程组求解，即可求出点A的坐标。
（2）利用勾股定理求出OA的长，根据已知点M在x轴上，且△AOM是等腰三角形，分四种情况讨论：当OM1=OA=5时，当OM2=OA=5时，当AM3=OA=5时，当OM4=AM4时，分别写出点M的坐标。
（3）根据已知点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），设出B与C坐标，表示出BC，由已知BC与OA关系，及OA的长求出BC的长，求出a的值，利用三角形的面积公式求出△ABC的面积，再求出a的值，即可确定出点B、C的坐标。
（4）作出D关于直线BC的对称点D′，连接AD′，与直线BC交于点E，连接DE，此时△ADE周长最小，先求出点D′的坐标，再求出直线直线AD′解析式，即可求出点E的坐标。
【考点精析】掌握三角形的面积和等腰三角形的性质是解答本题的根本，需要知道三角形的面积=1/2×底×高；等腰三角形的两个底角相等（简称：等边对等角）．
