Question

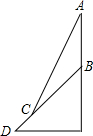如图甲，有一个塔高40米，位于一座山上，在其下方有一个坡度i=1：1的斜坡，某一时刻，身高1.60米的同学小明测得自己的影子（在平地上）为0.8米，那么，此时这个塔在斜坡上的影子长为多少米？（可借用图形乙）

Answer 1

分析：应转化成两个直角三角形求解．利用AE与BE的比为1：1；求得BE，进而求得CE长．然后根据小明的身高：影子长=2：1，得到BC长．

解答：解：过点C作CE⊥AE于E（如图）．
∵斜坡的坡度为i=1：1，
∴∠BCE=45度，
设BE=x，则CE=x，
∵AB=40，
∴AE=40+x，
∵这一时刻，身高1.60米的同学小明测得自己的影子（在平地上）为0.8米，
∴

AE

BE

=

1.6

0.8

=2，
即：

40+x

x

=2，得x=40．
∴这个塔在斜坡上的影子长为BC=40

2

米．

点评：这两个直角三角形有公共的直角边，先求出公共边的解决此类题目的基本出发点．