题目内容
现有边长为a的正方形花布，问怎样剪裁，才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝？
【答案】分析：当八边形为正八边形时面积最大，则要利用正八边形的边长相等和正方形花布的四个角各截去一个全等的直角三角形的性质，列式求解．
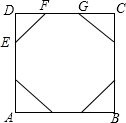
解答：解：如图，将正方形花布的四个角各截去一个全等的直角三角形
设DF=GC=x，则EF=
x
因为EF=FG，所以
x=a-2x，解得：x=
a
因此，应从正方形花布的四个角各截去一个全等的直角边
a的等腰直角三角形．
点评：主要考查了正方形的性质和等腰直角三角形的性质．注意正方形是特殊条件最多的特殊平行四边形．
解答：解：如图，将正方形花布的四个角各截去一个全等的直角三角形
设DF=GC=x，则EF=
x因为EF=FG，所以
x=a-2x，解得：x=a因此，应从正方形花布的四个角各截去一个全等的直角边
a的等腰直角三角形．点评：主要考查了正方形的性质和等腰直角三角形的性质．注意正方形是特殊条件最多的特殊平行四边形．
练习册系列答案
相关题目
20、如图，现有边长为a的正方形纸片1张、边长为b的正方形纸片2张，边长分别为a，b的长方形纸片3张，把它们拼成一个长方形．请利用此拼图中的面积关系，分解因式：a2+3ab+2b2=
现有边长为a的正方形花布，问怎样剪裁，才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝？