题目内容
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B。已知抛物线y=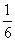 x2+bx+c过点A和B,与y轴交于点C。
x2+bx+c过点A和B,与y轴交于点C。
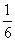 x2+bx+c过点A和B,与y轴交于点C。
x2+bx+c过点A和B,与y轴交于点C。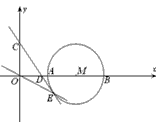
(1)求点C的坐标;
(2)点Q(8,m)在抛物线y=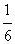 x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;
x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式。
(2)点Q(8,m)在抛物线y=
 x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;
x2+bx+c上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值;(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式。
解:(1)由已知,得A(2,0),B(6,0)
∵ 抛物线 过点A和B,则
过点A和B,则
 解得
解得
则抛物线的解析式为:
故 C(0,2);
(2)如图①,抛物线对称轴l是:x=4
∵Q(8,m)抛物线上
∴m=2
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6
∴AQ=
又∵B(6,0)与A(2,0)关于对称轴l对称
∴PQ+PB的最小值=AQ=
 ;
;
(3)如图②,连结EM和CM

由已知,得EM=OC=2,CE是⊙M的切线
∴∠DEM=90o,则∠DEM=∠DOC
又∵∠ODC=∠EDM
故△DEM≌△DOC
∴OD=DE,CD=MD
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC
则OE∥CM
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0)
∴ 解得
解得
直线CM的解析式为
又∵直线OE过原点O,且OE∥CM
则OE的解析式为y= x。
x。
∵ 抛物线
 过点A和B,则
过点A和B,则 解得
解得
则抛物线的解析式为:

故 C(0,2);
(2)如图①,抛物线对称轴l是:x=4
∵Q(8,m)抛物线上
∴m=2
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6
∴AQ=

又∵B(6,0)与A(2,0)关于对称轴l对称
∴PQ+PB的最小值=AQ=

 ;
;(3)如图②,连结EM和CM

由已知,得EM=OC=2,CE是⊙M的切线
∴∠DEM=90o,则∠DEM=∠DOC
又∵∠ODC=∠EDM
故△DEM≌△DOC
∴OD=DE,CD=MD
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC
则OE∥CM
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0)
∴
 解得
解得
直线CM的解析式为

又∵直线OE过原点O,且OE∥CM
则OE的解析式为y=
 x。
x。
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是