题目内容
在半径为2的⊙O中，弦AB的长为2，则弦AB所对的圆心角的度数为________度．
60
分析：连接OA、OB，可证得△OAB是等边三角形，由此得解．
解答：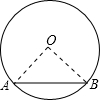
解：如图；连接OA、OB；
∵OA=OB=AB=2，
∴△OAB是等边三角形；
∴∠AOB=60°；
故弦AB所对的圆心角的度数为60°．
点评：此题考查的是圆心角、弦的关系，涉及的知识点有：等边三角形的判定和性质．
分析：连接OA、OB，可证得△OAB是等边三角形，由此得解．
解答：
解：如图；连接OA、OB；∵OA=OB=AB=2，
∴△OAB是等边三角形；
∴∠AOB=60°；
故弦AB所对的圆心角的度数为60°．
点评：此题考查的是圆心角、弦的关系，涉及的知识点有：等边三角形的判定和性质．
练习册系列答案
阅读快车系列答案
相关题目