题目内容
当k=________时,关于x的一元二次方程kx2-2(k+1)x+k-1=0的两个不相等的实数根x1,x2满足 .
.
5
分析:由于原方程有不相等的实数根,利用根与系数的关系,可求出x1+x2,x1x2的值,然后再代入 =3,即可求出k的值.
=3,即可求出k的值.
解答:根据题意得
x1+x2=- =-
=-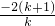 =
= ,
,
x1x2= =
=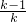 ,
,
又∵ =3,
=3,
∴ =
=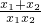 =
= ×
×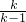 =
=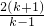 =3,
=3,
即2(k+1)=3(k-1),
解得k=5.
点评:本题利用了根与系数的关系,即一个一元二次方程ax2+bx+c=0的两个根x1、x2存在这样的关系:x1+x2=- ,x1x2=
,x1x2= .
.
分析:由于原方程有不相等的实数根,利用根与系数的关系,可求出x1+x2,x1x2的值,然后再代入
 =3,即可求出k的值.
=3,即可求出k的值.解答:根据题意得
x1+x2=-
 =-
=-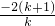 =
= ,
,x1x2=
 =
=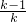 ,
,又∵
 =3,
=3,∴
 =
=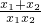 =
= ×
×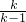 =
=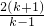 =3,
=3,即2(k+1)=3(k-1),
解得k=5.
点评:本题利用了根与系数的关系,即一个一元二次方程ax2+bx+c=0的两个根x1、x2存在这样的关系:x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目