题目内容
k为何值时,方程kx2-6x+9=0有:
(1)不等的两实根;
(2)相等的两实根;
(3)没有实根.
解:(1)∵方程有不等的两实根,
∴k≠0且△>0,即(-6)2-4k×9>0,
∴k<1且k≠0;
(2)∵方程有相等的两实根,
∴k≠0且△=0,即(-6)2-4k×9=0,
∴k=1;
(3)∵方程没有实根,
∴k≠0且△<0,即(-6)2-4k×9<0,
∴k>1.
分析:(1)根据△的意义方程有不等的两实根,则必有k≠0且△>0,即(-6)2-4k×9>0,然后求出两个不等式的公共部分即可;
(2)根据△的意义方程有相等的两实根,则必有k≠0且△=0,即(-6)2-4k×9=0,然后解关于k的方程即可.
(3)根据△的意义方程没有实根,则必有k≠0且△<0,即(-6)2-4k×9<0,然后求出两个不等式的公共部分即可.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.
∴k≠0且△>0,即(-6)2-4k×9>0,
∴k<1且k≠0;
(2)∵方程有相等的两实根,
∴k≠0且△=0,即(-6)2-4k×9=0,
∴k=1;
(3)∵方程没有实根,
∴k≠0且△<0,即(-6)2-4k×9<0,
∴k>1.
分析:(1)根据△的意义方程有不等的两实根,则必有k≠0且△>0,即(-6)2-4k×9>0,然后求出两个不等式的公共部分即可;
(2)根据△的意义方程有相等的两实根,则必有k≠0且△=0,即(-6)2-4k×9=0,然后解关于k的方程即可.
(3)根据△的意义方程没有实根,则必有k≠0且△<0,即(-6)2-4k×9<0,然后求出两个不等式的公共部分即可.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ;
; ;
; ;
;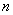 个数:
个数: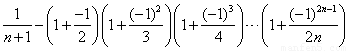 .
. ,
, ,求ab的值。
,求ab的值。