Question

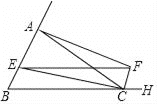
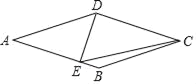
【题目】如图，菱形ABCD中，DE⊥AB，垂足为点E，连接CE．若AE＝2，∠DCE＝30°，则菱形的边长为________．

Answer 1

【答案】

【解析】

由四边形ABCD为菱形性质得DC∥AB，则同旁内角互补，得∠CDE+∠DEB=180°，

结合DE⊥AB，则DE⊥DC，已知∠DCE=30°，设DE=x, 用勾股定理把DC、AD、和DE用含x的代数式表示，在Rt△AED中，利用勾股列关系式求得x=， 则.

解：∵四边形ABCD为菱形，

∴DC∥AB，

∴∠CDE+∠DEB=180°，

∵DE⊥AB，

∴DE⊥DC，

∵∠DCE=30°，

设DE=x, 则EC=2x，

，

∴AD=DC=，

在Rt△AED中，有AD2=DE2+AE2 ，

解得x=，

，

故答案为：.