题目内容
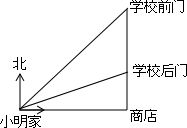 如图,小明家到学校有两条路,一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东,到商店处向正北走100米,到学校后门;若两条路程相等,学校南北走向,学校后门在小明家北偏东67.5°处,学校前门到后门的距离是( )
如图,小明家到学校有两条路,一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东,到商店处向正北走100米,到学校后门;若两条路程相等,学校南北走向,学校后门在小明家北偏东67.5°处,学校前门到后门的距离是( )| A、100米 | ||
B、100
| ||
C、200
| ||
D、100
|
分析:易得∠CAB为45°,那么利用45°的余弦值可得AB的长,也就是BC的长,减去100即为所求的距离.
解答: 解:由题意得∠CAB=45°,AB+100=AC,
解:由题意得∠CAB=45°,AB+100=AC,
∵cos∠CAB=
=
,
∴AB=100
+100,
∴BC=AB=100
+100,
∴CD=100
米.
故选B.
 解:由题意得∠CAB=45°,AB+100=AC,
解:由题意得∠CAB=45°,AB+100=AC,∵cos∠CAB=
| ||
| 2 |
| AB |
| AC |
∴AB=100
| 2 |
∴BC=AB=100
| 2 |
∴CD=100
| 2 |
故选B.
点评:本题考查解直角三角形的应用;综合利用题中所给条件得到AB的长是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,小明家到学校有两条路,一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东,到商店处向正北走100米,到学校后门;若两条路程相等,学校南北走向,学校后门在小明家北偏东67.5°处,学校前门到后门的距离是
如图,小明家到学校有两条路,一条沿北偏东45°方向可直达学校前门,另一条从小明家一直往东,到商店处向正北走100米,到学校后门;若两条路程相等,学校南北走向,学校后门在小明家北偏东67.5°处,学校前门到后门的距离是 米
米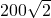 米
米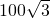 米
米
 米
米 米
米 米
米
 米
米 米
米 米
米
 米
米 米
米 米
米