题目内容
 如图,双曲线y=
如图,双曲线y= 经过Rt△OMN斜边上的点A,与直角边MN交于点B,已知OA=2AN,△OAB的面积为
经过Rt△OMN斜边上的点A,与直角边MN交于点B,已知OA=2AN,△OAB的面积为 ,则k的值是
,则k的值是
- A.4
- B.5
- C.6
- D.7
C
分析:作AE⊥x轴于E,AF⊥y轴于F,设N的坐标是(a,b),根据相似三角形的性质即可表示出A的坐标,从而利用a,b表示出k的值,求得B的坐标,则△OAB的面积即可利用a,b表示出来,从而求得ab的值,则k的值即可求得.
解答: 解:作AE⊥x轴于E,AF⊥y轴于F.
解:作AE⊥x轴于E,AF⊥y轴于F.
则AE∥MN,
∴△AOE∽△NOM,
∴ =
= =
= ,即AE=
,即AE= MN,OE=
MN,OE= OM,
OM,
同理:NF= MN,MF=
MN,MF= MN,
MN,
设N的坐标是(a,b),则A的坐标是( a,
a, b),
b),
代入y= 得:k=
得:k= ab,
ab,
在y= 中,令x=a,则y=
中,令x=a,则y= ,故B的坐标是:(a,
,故B的坐标是:(a, b),即BM=
b),即BM= ,NB=b-
,NB=b- =
= .
.
∴S△OBM= OM•BM=
OM•BM= a•
a• =
= ,
,
S△ABN= BN•AF=
BN•AF= ×
× ×
× a=
a= ,
,
又∵S△OMN= ab,
ab,
∴S△OAB= ab-
ab- -
- =
=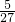 ab=
ab= ,
,
∴ab= .
.
∴k= ×
× =6.
=6.
故选C.
点评:本题是待定系数法求函数的解析式,相似三角形的判定与性质的综合应用,正确表示出B的坐标是关键.
分析:作AE⊥x轴于E,AF⊥y轴于F,设N的坐标是(a,b),根据相似三角形的性质即可表示出A的坐标,从而利用a,b表示出k的值,求得B的坐标,则△OAB的面积即可利用a,b表示出来,从而求得ab的值,则k的值即可求得.
解答:
 解:作AE⊥x轴于E,AF⊥y轴于F.
解:作AE⊥x轴于E,AF⊥y轴于F.则AE∥MN,
∴△AOE∽△NOM,
∴
 =
= =
= ,即AE=
,即AE= MN,OE=
MN,OE= OM,
OM,同理:NF=
 MN,MF=
MN,MF= MN,
MN,设N的坐标是(a,b),则A的坐标是(
 a,
a, b),
b),代入y=
 得:k=
得:k= ab,
ab,在y=
 中,令x=a,则y=
中,令x=a,则y= ,故B的坐标是:(a,
,故B的坐标是:(a, b),即BM=
b),即BM= ,NB=b-
,NB=b- =
= .
.∴S△OBM=
 OM•BM=
OM•BM= a•
a• =
= ,
,S△ABN=
 BN•AF=
BN•AF= ×
× ×
× a=
a= ,
,又∵S△OMN=
 ab,
ab,∴S△OAB=
 ab-
ab- -
- =
=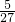 ab=
ab= ,
,∴ab=
 .
.∴k=
 ×
× =6.
=6.故选C.
点评:本题是待定系数法求函数的解析式,相似三角形的判定与性质的综合应用,正确表示出B的坐标是关键.

练习册系列答案
相关题目
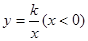 经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥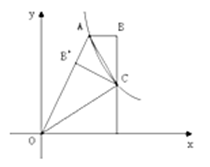
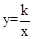 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .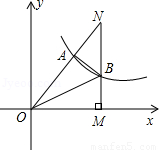
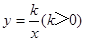 经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .
经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .