题目内容
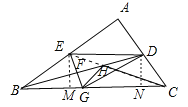
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
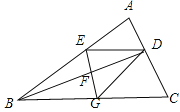
【答案】(1)四边形EBGD是菱形;(2)10.
【解析】
试题分析:(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,∴EB=ED,GB=GD,∴∠EBD=∠EDB,∵∠EBD=∠DBC,∴∠EDF=∠GBF,在△EFD和△GFB中,∵∠EDF=∠GBF,∠EFD=∠GFB,DF=BF,∴△EFD≌△GFB,∴ED=BG,∴BE=ED=DG=GB,∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=![]() ,∴EM=
,∴EM=![]() BE=
BE=![]() ,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=
,∵DE∥BC,EM⊥BC,DN⊥BC,∴EM∥DN,EM=DN=![]() ,MN=DE=
,MN=DE=![]() ,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=
,在RT△DNC中,∵∠DNC=90°,∠DCN=45°,∴∠NDC=∠NCD=45°,∴DN=NC=![]() ,∴MC=
,∴MC=![]() ,在RT△EMC中,∵∠EMC=90°,EM=
,在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=
.MC=![]() ,∴EC=
,∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,∴HG+HC的最小值为10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目