题目内容
如图，点A所表示的数是（ ）分析：利用勾股定理求出OB的长度，继而得出OA的长度，根据点O表示的数为0，可得出点A表示的数．
解答：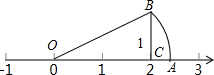
解：由题意得，OC=2，BC=1，
在RT△OBC中，OB=
=
，
故可得OA=OB=
，即点A表示的数为
．
故选D．
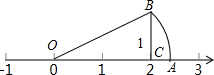
解：由题意得，OC=2，BC=1，
在RT△OBC中，OB=
| OC2+BC2 |
| 5 |
故可得OA=OB=
| 5 |
| 5 |
故选D．
点评：此题考查了勾股定理的知识，属于基础题，利用勾股定理求出OB的长度是解答本题的关键，难度一般．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，点A所表示的数是（ ）| A、1.5 | ||
B、
| ||
| C、2 | ||
D、
|
如图，点A所表示的数是（ ） 
| A．1.5 | B． | C．2 | D． |
C．2 D．
如图，点A所表示的数是
