题目内容
已知方程:x2﹣2x﹣8=0,解决一下问题:
(1)不解方程判断此方程的根的情况; 请按要求分别解这个方程:①配方法;②因式分解法.
(3)这些方法都是将解 转化为解 ;
(4)尝试解方程:x3+2x2+x=0.
【考点】根的判别式;解一元二次方程-配方法;解一元二次方程-因式分解法.
【分析】(1)由 a=1,b=﹣2,c=﹣8,可得△=b2﹣4ac=36>0,即可判定此方程的根的情况;
①直接利用配方法解一元二次方程;②利用十字相等法解一元二次方程;
(3)利用消元法,将解一元二次方程转化为解一元一次方程;
(4)利用因式分解法求解即可求得答案.
【解答】解:(1)∵a=1,b=﹣2,c=﹣8,
∴△=b2﹣4ac=(﹣2)2﹣4×1×(﹣8)=36>0,
∴此方程有两个不相等的实数根;
①配方法:∵x2﹣2x﹣8=0,
∴x2﹣2x=8,
∴x2﹣2x+1=8+1,
∴(x﹣1)2=9,
∴x﹣1=±3, 解得:x1=4,x2=﹣2;
②因式分解法:∵x2﹣2x﹣8=0,
∴(x﹣4)(x+2)=0, 解得:x1=4,x2=﹣2;
(3)答案为:一元二次方程;一元一次方程;
(4)∵x3+2x2+x=0,
∴x(x2+2x+1)=0,
∴x(x+1)2=0,
∴x=0,x+1=0, 解得:x1=0,x2=x3=﹣1.
【点评】此题考查了一元二次方程的解法以及根的判别式.注意△>0⇔方程有两个不相等的实数根.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目




 在 、
在 、  、
、  、 、 中,是最简二次根式的是 .
、 、 中,是最简二次根式的是 .

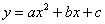 (
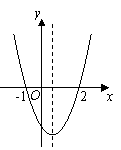
(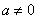 )的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )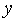 随
随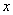 的增大而减少
的增大而减少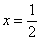 D、当
D、当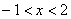 时,
时,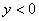
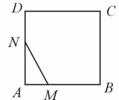
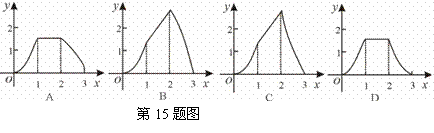
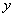 (cm2),运动时间为
(cm2),运动时间为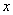 (秒),则下列图象中能大致反映
(秒),则下列图象中能大致反映