题目内容
如图AB为⊙O的直径，弦AB⊥CD，垂足为P，BP=2，CD=16，求直径AB的长．分析：先根据已知条件得出PC的长，再连接OC，设⊙O的半径为r，在Rt△OCP中利用勾股定理即可求出R的值，进而得出结论．
解答：
解：∵AB为⊙O的直径，弦AB⊥CD，CD=16，
∴PC=
CD=
×16=8，
连接OC，设⊙O的半径为R，则OP=r-PB=r-2，
在Rt△OCP中，
OC2=OP2+PC2，即r2=82+（r-2）2，解得r=17，
∴AB=2r=2×17=34．
解：∵AB为⊙O的直径，弦AB⊥CD，CD=16，∴PC=
| 1 |
| 2 |
| 1 |
| 2 |
连接OC，设⊙O的半径为R，则OP=r-PB=r-2，
在Rt△OCP中，
OC2=OP2+PC2，即r2=82+（r-2）2，解得r=17，
∴AB=2r=2×17=34．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
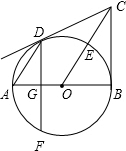如图AB为⊙O的直径，BC⊥AB于点B，连接OC交⊙O于E，弦AD∥OC，弦DF⊥AB于点G．
9、如图AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，连接AC，BC，则与∠ACD互余的角有（ ）
如图AB为⊙O的直径，C为半圆AB上一点，过C作CD⊥AB交圆于点D，CP平分∠DOC，当C在半圆AB上运动时，则点P（ ）
如图AB为⊙O的直径，C、D是⊙O上两点，若∠ABC=55°，则∠D的度数为