题目内容

如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：根据边长为4的等边△ABC中，DE为中位线，得出DF= $\text{[math]}$ ，再利用梯形的面积公式求出．
解答：

解：作DF⊥BC，
∵边长为4的等边△ABC中，DE为中位线，
∴DE=2，BD=2，
∴DF=BD•sin∠B=2× $\text{[math]}$ = $\text{[math]}$ ，
∴四边形BCED的面积为： $\text{[math]}$ DF×（DE+BC）= $\text{[math]}$ × $\text{[math]}$ （2+4）=3 $\text{[math]}$ ．
故选B．
点评：此题主要考查了等边三角形的性质以及三角形中位线的性质，根据DE为中位线，得出DF= $\text{[math]}$ 是解决问题的关键．

练习册系列答案

黄冈重点中学名师编写金卷100分系列答案

精致小卷专为小科金卷100分系列答案

课课精练优学优练系列答案

奥数典型题举一反三系列答案

帮你学单元目标检测题AB卷系列答案

精彩练习就练这一本系列答案

名校调研期末冲刺系列答案

能力评价系列答案

唐印文化课时测评系列答案

小学霸系列答案

相关题目

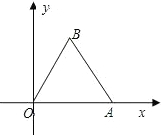如图，边长为2的等边三角形OAB的顶点A在x轴的正半轴上，B点位于第一象限，将△OAB绕点O顺时针旋转30°后，恰好点A落在双曲线y=

（x＞0）上，如果等边三角形OAB的A点再次落在双曲线上，那么应继续至少按顺时针旋转

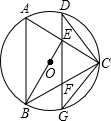如图，边长为4的等边三角形ABC内接于⊙O，直线EF经过边AC，BC的中点，交⊙O于D、G两点．
（1）求证：△CED≌△CFG；
（2）设ED=a，EB=b，问：在线段EF上是否存在点M，EM的长m能使

的解？若存在，求二次函数y=px2-2px+

的最大值或最小值；若不存在，说明理由．

如图，边长为2的等边△ABC，射线AB上有一点动P（P不与点A、点B重合），以PC为边作等边△PDC，点D与点A在BC同侧，E为AC中点，连接AD、PE、ED．

（1）试探讨四边形ABCD的形状，并说明理由．
（2）当点P在线段AB上运动，（不与点A、点B重合），若BP=x，四边形APED的面积是否为定值呢？请说明理由．
（3）在第（2）问的条件下，若BP=x，△PDE的面积为y，求出y与x之间的函数关系式，并求出△PDE的面积的最小值，及取得最小值时x的取值．

（1997•南京）已知：如图，边长为2的等边三角形ABC，延长BC到D，使CD=BC，延长CB到E，使BE=CB，求△ADE的周长．

（2013•福州质检）如图，边长为6的等边三角形ABC中，E是对称轴AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E运动过程中，DF的最小值是