题目内容
已知：如图，AE是⊙O的直径，AF⊥BC于D，证明：BE=CF．分析：若要证明BE=CF，则可转化为证∠BAE=∠FAC即可，根据圆周角定理和等角的余角相等证明即可．
解答：证明：∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠E+∠BAE=90°，
∵AF⊥BC于D，
∴∠FAC+∠ACB=90°，
∵∠E=∠ACB，
∴∠BAE=∠FAC，
∴弧BE=弧CF，
∴BE=CF．
∴∠ABE=90°，
∴∠E+∠BAE=90°，
∵AF⊥BC于D，
∴∠FAC+∠ACB=90°，
∵∠E=∠ACB，
∴∠BAE=∠FAC，
∴弧BE=弧CF，
∴BE=CF．
点评：本题考查了圆周角定理和其推论：：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
练习册系列答案
相关题目
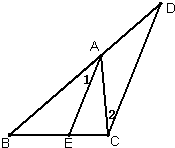26、已知，如图，AE是∠BAC的平分线，∠1=∠D．
已知，如图，AE是∠BAC的平分线，∠1=∠D．
