题目内容
 如图,D是△ABC的AB边上一点,过D作DE∥BC,交AC于E,已知AD:AB=1:2,那么S△ADE:S△ABC的值为
如图,D是△ABC的AB边上一点,过D作DE∥BC,交AC于E,已知AD:AB=1:2,那么S△ADE:S△ABC的值为
- A.4:9
- B.2:3
- C.1:4
- D.1:2
C
分析:相似三角形的面积比等于相似比的平方即可求.
解答:∵DE∥BC,
∴△ADE∽△ABC,
又∵AD:AB=1:2,
∴S△ADE:S△ABC的值为1:4.
故选C
点评:本题主要考查了平行于三角形一边的直线截得的三角形与原三角形相似,相似三角形对应边的比相等.
分析:相似三角形的面积比等于相似比的平方即可求.
解答:∵DE∥BC,
∴△ADE∽△ABC,
又∵AD:AB=1:2,
∴S△ADE:S△ABC的值为1:4.
故选C
点评:本题主要考查了平行于三角形一边的直线截得的三角形与原三角形相似,相似三角形对应边的比相等.

练习册系列答案
相关题目
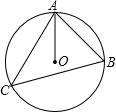 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
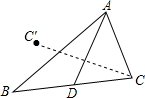 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=