题目内容
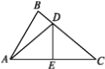
【题目】(1)阅读理解:如图1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 边上的中线
边上的中线![]() 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() .利用全等将边
.利用全等将边![]() 转化到
转化到![]() ,在
,在![]() 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线![]() 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线![]() 的取值范围是__________.
的取值范围是__________.
(2)问题解决:如图2,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,若
边上,若![]() .求证:
.求证:![]() .
.
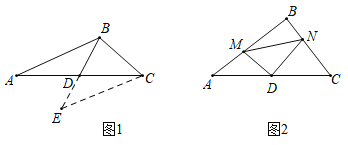
【答案】(1)![]() ,
,![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,先证明
,先证明![]() ,得到
,得到![]() ,再由三角形的三边关系即可解答.
,再由三角形的三边关系即可解答.
(2)连![]() ,并延长
,并延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连
,连![]() ,由(1)先证明
,由(1)先证明![]() ,得到
,得到![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() 是线段
是线段![]() 的垂直平分线,所以
的垂直平分线,所以![]() ,然后三角形三边关系即可解答.
,然后三角形三边关系即可解答.
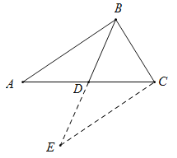
(1)解:如图,延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,
,
∵![]() 是
是![]() 边上的中线,
边上的中线,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由三角形的三边关系得:
中,由三角形的三边关系得:![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)如图,连![]() ,并延长
,并延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连
,连![]() ,
,

由(1)可知![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
在![]() 中,由三边关系得
中,由三边关系得![]() ,
,
∴![]() .
.

练习册系列答案
相关题目