题目内容
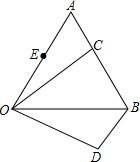
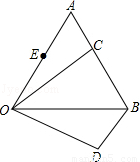
如图,△AOB是等边三角形,C为AB上一点,△OAC沿顺时针方向旋转后到达△OBD的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果点E为OA的中点,那么经过上述旋转后,点E旋转到了什么位置?
【答案】
(1)点O (2)60度 (3)OB的中点处
【解析】
试题分析:(1)点O在旋转中位置不变,因而是旋转中心;
(2)旋转角是∠AOB,根据等边三角形的性质即可确定;
(3)以O为圆心,以OE为半径,与OB的交点就是所求的点,即为OB的中点.
解:∵△AOB是等边三角形,
∴OA=OB,∠AOB=60°,
∵△OAC沿顺时针方向旋转后到达△OBD的位置,
∴OA旋转到OB,旋转角为∠AOB.
(1)旋转中心是点O;
(2)旋转了60度;
(3)如果点E为OA的中点,那么经过上述旋转后,点E旋转到了OB的中点处.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等,对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
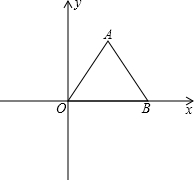 如图,△AOB是等边三角形,点O是坐标原点,点B的坐标为(2,0)
如图,△AOB是等边三角形,点O是坐标原点,点B的坐标为(2,0)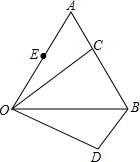 如图,△AOB是等边三角形,C为AB上一点,△OAC沿顺时针方向旋转后到达△OBD的位置.
如图,△AOB是等边三角形,C为AB上一点,△OAC沿顺时针方向旋转后到达△OBD的位置. 如图,△AOB是等边三角形,点O是坐标原点,点B的坐标为(2,0)
如图,△AOB是等边三角形,点O是坐标原点,点B的坐标为(2,0)